Program linear mungkin merupakan salah satu teknik yang digunakan paling luas dan diketahui dengan baik. Merupakan metode matematik dalam menglokasikan sumber daya yang terbatas untuk mencapai suatu tujuan seperti memaksimumkan keuntungan dan meminimumkan biaya. Program linear banyak diterapkan dalam masalah - masalah ekonomi, industri, militer, sosial dan lain – lain. Program linear berkaitan dengan penjelasan suatu dunia nyata sebagai suatu model matematik yang terdiri dari sebuah fungsi tujuan Linear dan beberapa kendala linear. Tahapan awal dalam penerapan – penerapan program linear banyak dijumpai pada masalah – masalah militer seperti logistik, transportasi, perbekalan. Kemudian program linear segera diterapkan dalam masalah – masalah sektor pemerintahan dan swasta dalam industri. Salah satu penerapannya di sektor industri adalah perusahaan konveksi yang ingin mendapatkan keuntungan maksimum. Dengan menggunakan program lienar maka perusahaan dapat mengetahui berapa jumlah produk yang harus di hasilkan untuk mendapatkan keuntungan maksimum.
Program linear mungkin merupakan salah satu teknik yang digunakan paling luas dan diketahui dengan baik. Merupakan metode matematik dalam menglokasikan sumber daya yang terbatas untuk mencapai suatu tujuan seperti memaksimumkan keuntungan dan meminimumkan biaya. Program linear banyak diterapkan dalam masalah - masalah ekonomi, industri, militer, sosial dan lain – lain. Program linear berkaitan dengan penjelasan suatu dunia nyata sebagai suatu model matematik yang terdiri dari sebuah fungsi tujuan Linear dan beberapa kendala linear. Tahapan awal dalam penerapan – penerapan program linear banyak dijumpai pada masalah – masalah militer seperti logistik, transportasi, perbekalan. Kemudian program linear segera diterapkan dalam masalah – masalah sektor pemerintahan dan swasta dalam industri. Salah satu penerapannya di sektor industri adalah perusahaan konveksi yang ingin mendapatkan keuntungan maksimum. Dengan menggunakan program lienar maka perusahaan dapat mengetahui berapa jumlah produk yang harus di hasilkan untuk mendapatkan keuntungan maksimum.
Secara umum Linear Programming ialah salah satu teknik dari Riset Operasi untuk memecahkan persoalan optimasi (maksimasi atau minimasi) dengan menggunakan persamaan dan ketidaksamaan linear dalam rangka untuk mencari pemecahan yang optimum dengan memperhatikan pembatasan-pembatasan yang ada. Dalam keadaan sumber yang terbatas harus dicapai suatu hasil yang optimum dengan perkataan lain bagaimana caranya agar dengan masukan input yang terbatas dapat menghasilkan keluaran output berupa produksi barang atau jasa yang optimum. Salah satu metoda analisis dalam teknik operasional riset untuk menyelesaikan persoalan pengalokasian sumber-sumber terbatas adalah menggunakan metoda program linear. Linear programming akan memberikan banyak sekali hasil pemecahan persoalan, sebagai alternatif pengambilan tindakan, akan tetapi hanya ada satu yang optimum (maksimum atau minimum). Memilih keputusan berarti memilh alternatif, tapi yang terpenting adalah pengambilan alternatif terbaik( the bestalternative),Johannes Suprapto (1987).
Menurut Hari Purnomo(2004) Pokok pikiran utama dalam menggunakan program linier adalah merumuskan masalah dengan menggunakan sejumlah informasi yang tersedia, kemudian menerjemahkan masalah tersebut dalam bentuk model matematika. Sifat linear mempunyai arti bahwa seluruh fungsi dalam model ini merupakan fungsi yang linear.
Menurut Ayu (1997), dalam metode transportasi terdapat beberapa cara untuk memecahkan permasalahn yang timbul. Metode tersebut antara lain:
a.Metode Northwest Corner
Metode ini digunakan untuk menyelesaikan permasalahan transportasi dengan cara pengalokasian yang dimulai dari kotak paling kiri atas yaitu pengalokasian sebanyak mungkin selama tidak melanggar batasan yang ada, yaitu sejumlah supply dan demandnya. Pengalokasian dilakukan menurun kebawah setelah itu ke kolom berikutnya sampai terpenuhi seluruh supply dan demandnya.
b.Metode Least Cost
Metode ini adalah metode yang pengalokasiannya dimulai pada kotak dengan biaya terendah dan dilanjutkan dengan kotak biaya terendah selanjutnya yang belum terpenuhi nilai demand dan supplynya.
c.Metode Aproximasi Vogel (VAM)
Vogel Approximation Method (VAM) yang dikembangkan oleh Vogel pada prinsipnya mencari opportunity cost (biaya peluang). Metode ini adalah metode yang pengalokasiannya dimulai dengan menentukan nilai selisih antara kotak dengan biaya terendah dan kotak dengan biaaya terendah berikutnya untuk setiap baris dan kolom (selajutnya kita sebut nilai selisih atau nilai penalty). Selajutnya dipilih baris atau kolom dengan nilai selisih terbesar, dan dilakukan pengalokasian pada kotak dengan biaya terendah pada baris/ kolom yang terpilih.
d.Metode Aproksimasi Russel
Metode ini adalah suatu metode yang pengalokasiannya dimulai dengan menetukan nilai u1 untuk setiap baris yang masih mungkin dilakukan pengalokasian dan nilai V1 untuk setiap kolom yang masing mungkin dilakukan pengalokasian. Nilai u1 yang biaya terbesar pada suatau baris dari kotak-kotak yang masih dilakukan pengalokasian, nilai V1 adalah biaya terbesar pada suatu kolom dari kotak-kotak yang masih dilakukan pengalokasian. Kemudian dilakukan perhitungan nilai untuk setiap kotak yang masih mungkin dilakukan pengalokasian. Selanjutnya dipilih kotak dengan nilai negatif terbesar dan dilakukan pengalokasian terhadap kotak tersebut.
Umumnya masalah transportasi berhubungan dengan distribusi suatu produk tunggal dari beberapa sumber, dengan penawaran terbatas menuju beberapa tujuan dengan permintaan tertentu pada biaya transportasi minimum. Karena hanya ada satu macam barang, suatu tempat tujuan dapat memenuhi permintaannya dari satu atau lebih sumber.
Asumsi dasar model ini adalah bahwa biaya transport pada suatu rute tertentu proposional dengan banyaknya unit yang dikirimkan. Definisi unit yang dikirimkan sangat tergantung pada jenis produk yang diangkut. Metode transportasi digunakan untuk menyelesaikan masalah-masalah dunia usaha bisnis, seperti masalah-masalah yang meliputi pengiklanan pembelanjaan modal, dan alalokasi dana untuk investasi, analisis lokasi, keseimbangan lini perakitan dan perncanaan serta schedluling produksi.
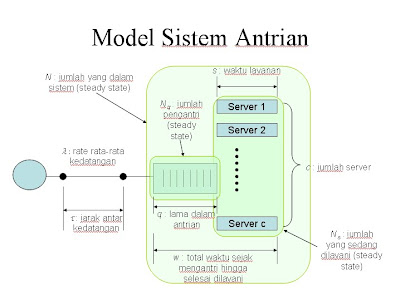
Ada tiga komponen dalam sistim antrian yaitu : 1. Kedatangan , populasi yang akan dilayani (calling population) Karakteristik dari populasi yang akan dilayani (calling population) dapat dilihat menurut ukurannya, pola kedatangan, serta perilaku dari populasi yang akan dilayani. Menurut ukurannya, populasi yang akan dilayani bisa terbatas (finite) bisa juga tidak terbatas (infinite). Sebagai contoh jumlah mahasiswa yang antri untuk registrasi di sebuah perguruan tinggi sudah diketahui jumlahnya (finite), sedangkan jumlah nasabah bank yang antri untuk setor, menarik tabungan, maupun membuka rekening baru, bisa tak terbatas (infinte). Pola kedatangan bisa teratur, bisa juga acak (random). Kedatangan yang teratur sering kita jumpai pada proses pembuatan/ pengemasan produk yang sudah distandardisasi. Pada proses semacam ini, kedatangan produk untuk diproses pada bagian selanjutnya biasanya sudah ditentukan waktunya, misalnya setiap 30 detik. Sedangkan pola kedatangan yang sifatnya acak (random) banyak kita jumpai misalnya kedatangan nasabah di bank. Pola kedatangan yang sifatnya acak dapat digambarkan dengan distribusi statistik dan dapat ditentukan dua cara yaitu kedatangan per satuan waktu dan distribusi waktu antar kedatangan.
2. Antrian Batasan panjang antrian bisa terbatas (limited) bisa juga tidak terbatas (unlimited). Sebagai contoh antrian di jalan tol masuk dalam kategori panjang antrian yang tidak terbatas. Sementara antrian di rumah makan, masuk kategori panjang antrian yang terbatas karena keterbatasan tempat. Dalam kasus batasan panjang antrian yang tertentu (definite line-length) dapat menyebabkan penundaan kedatangan antrian bila batasan telah tercapai. Contoh : sejumlah tertentu pesawat pada landasan telah melebihi suatu kapasitas bandara, kedatangan pesawat yang baru dialihkan ke bandara yang lain.
3. Fasilitas Pelayanan Karakteristik fasilitas pelayanan dapat dilihat dari tiga hal, yaitu tata letak (lay out) secara fisik dari sistem antrian, disiplin antrian, waktu pelayanan.
Tata letak Tata letak fisik dari sistem antrian digambarkan dengan jumlah saluran, juga disebut sebagai jumlah pelayan. Sistem antrian jalur tunggal (single channel, single server) berarti bahwa dalam sistem antrian tersebut hanya terdapat satu pemberi layanan serta satu jenis layanan yang diberikan. Sementara sistem antrian jalur tunggal tahapan berganda (single channel multi server) berarti dalam sistem antrian tersebut terdapat lebih dari satu jenis layanan yang diberikan, tetapi dalam setiap jenis layanan hanya terdapat satu pemberi layanan. Sistem antrian jalur berganda satu tahap (multi channel single server) adalah terdapat satu jenis layanan dalam sistem antrian tersebut , namun terdapat lebih dari satu pemberi layanan. Sedangkan sistem antrian jalur berganda dengan tahapan berganda (multi channel, multi server) adalah sistem antrian dimana terdapat lebih dari satu jenis layanan dan terdapat lebih dari satu pemberi layanan dalam setiap jenis layanan.
Disiplin antrian Ada dua klasifikasi yaitu prioritas dan first come first serve. Disiplin prioritas dikelompokkan menjadi dua, yaitu preemptive dan non preemptive. Disiplin preemptive menggambarkan situasi dimana pelayan sedang melayani seseorang, kemudian beralih melayani orang yang diprioritaskan meskipun belum selesai melayani orang sebelumnya. Sementara disiplin non preemptive menggambarkan situasi dimana pelayan akan menyelesaikan pelayanannya baru kemudian beralih melayani orang yang diprioritaskan. Sedangkan disiplin first come first serve menggambarkan bahwa orang yang lebih dahulu datang akan dilayani terlebih dahulu.
Waktu Pelayanan Karakteristik waktu pelayanan. Waktu yang dibutuhkan untuk melayani bisa dikategorikan sebagai konstan dan acak. Waktu pelayanan konstan, jika waktu yang dibutuhkan untuk melayani sama untuk setiap pelanggan. Sedangkan waktu pelayanan acak, jika waktu yang dibutuhkan untuk melayani berbeda-beda untuk setiap pelanggan. Jika waktu pelayanan acak, diasumsikan mengikuti distribusi eksponensial.
Terkadang, antrian yang sangat panjang dan terlalu lama untuk memperoleh giliran pelayanan membuat kita merasa kesal. Kecepatan rata-rata pelayanan mempegaruhi lamanya waktu menunggu. Teori tentang antrian pertamakali diketemukan dan dikembangkan oleh A.K. Erlang, seorang insinyur dari Denmark yang bekerja pada perusahaan telepon di Kopenhagen pada tahun 1910. Eksperimen yang dilakukannya adalah tentang fluktuasi permintaan fasilitas telepon yang berhubungan dengan automatic dialing equipment, yaitu peralatan penyambungan telepon secara otomatis. Pada waktu sibuk, operator kewalahan untuk melayani penelpon, sehingga membuat penelpon menunggu. Awalnya, Erlang hanya melakukan perhitungan keterlambatan (delay) dari seorang operator, kemudian pada tahun 1917 penelitian dilanjutkan untuk menghitung kesibukan beberapa operator. Masih dalam tahun yang sama, Erlang menerbitkan bukunya yang terkenal berjudul Solution of some problems in the theory of probabilities of significance in Automatic Telephone Exhange. Baru setelah perang dunia kedua, hasil penelitian Erlang diperluas penggunaannya antara lain dalam teori antrian (Supranto, 1987).
Antrian yang panjang sering kali kita lihat di bank saat nasabah mengantri di teller untuk melakukan transaksi, airport saat pesawat menunggu antrian untuk landing, di super market saat orang berbelanja antri untuk melakukan pembayaran, di tempat cuci mobil : mobil antri untuk dicuci dan masih banyak contoh lainnya. Di sektor jasa, bagi sebagian orang antri merupakan hal yang membosankan dan sebagai akibatnya terlalu lama antri, akan menyebabkan pelanggan kabur. Hal ini merupakan kerugian bagi organisasi tersebut. Untuk mempertahankan pelanggan, sebuah perusahaan selalu berusaha untuk memberikan pelayanan yang terbaik. Pelayanan yang terbaik tersebut diantaranya adalah memberikan pelayanan yang cepat sehingga pelanggan tidak dibiarkan menunggu (mengantri) terlalu lama. Namun demikian, dampak pemberian layanan yang cepat ini akan menimbulkan biaya bagi organisasi, karena harus menambah fasilitas layanan. Oleh karena itu, layanan yang cepat akan sangat membantu untuk mempertahankan pelanggan, yang dalam jangka panjang tentu saja akan meningkatkan keuntungan perusahaan.
Salah satu model yang sangat berkembang sekarang ini ialah model matematika. Umumnya, solusi untuk model matematika dapat dijabarkan berdasarkan dua macam prosedur, yaitu : analitis dan simulasi. Pada model simulasi, solusi tidak dijabarkan secara deduktif. Sebaliknya, model dicoba terhadap harga – harga khusus variabel jawab berdasarkan syarat– syarat tertentu (sudah diperhitungkan terlebih dahulu), kemudian diselidiki pengaruhnya terhadap variabel kriteria. Karena itu, model simulasi pada hakikatnya mempunyai sifat induktif. Misalnya dalam persoalan antrian, dapat dicoba pengaruh bermacam – macam bentuk sistem pembayaran sehingga diperoleh solusi untuk situasi atau syarat pertibaan yang mana pun.
Penyelesaian dilakukan dengan menggunakan konsep maksimin untuk pemain baris dan minimaks untuk pemain kolom. Dalam strategi ini pemain akan menggunakan satu strategi tunggal untuk mendapat hasil optimal.
STRATEGI CAMPURAN
Strategi ini dilakukan bila strategi murni belum memberi penyelesaian optimal. Sehingga perludilakukan tindak lanjut untuk mendapat titik optimal, dengan usaha mendapatkan saddle point yang sama.
Dalam teori permainan ada ketentuan umum yang berlaku yaitu :
Setiap pemain bermain rasional, dengan asumsi memiliki intelegensi yang sama, dan tujuan sama, yaitu memaksimumkan payoff, dengan kriteria maksimin dan minimaks.
2.Terdiri dari 2 pemain, keuntungan bagi salah satu pemain merupakan kerugian bagi pemain lain.
3.Tabel yang disusun menunjukkan keuntungan pemain baris, dan kerugian pemain kolom.
4.Permainan dikatakan adil jika hasil akhir menghasilkan nilai nol (0), tidak ada yang menang/kalah.
5.Tujuan dari teori permainan ini adalah mengidentifikasistrategi yang paling optimal
Teori permainan adalah suatu cara belajar yang digunakan dalam menganalisa interaksi antara sejumlah pemain maupun perorangan yang menunjukkan strategi-strategi yang rasional. Teori permainan pertama kali ditemukan oleh sekelompok ahli Matematika pada tahun 1944. Teori itu dikemukakan oleh John von Neumann and Oskar Morgenstern yang berisi : “Permainan terdiri atas sekumpulan peraturan yang membangun situasi bersaing dari dua sampai beberapa orang atau kelompok dengan memilih strategi yang dibangun untuk memaksimalkan kemenangan sendiri atau pun untuk meminimalkan kemenangan lawan. Peraturan-peraturan menentukan kemungkinan tindakan untuk setiap pemain, sejumlah keterangan diterima setiap pemain sebagai kemajuan bermain, dan sejumlah kemenangan atau kekalahan dalam berbagai situasi.” Teori permainan kemudian dikembangkan oleh ilmuan Prancis bernama Emile Borel ini, secara umum digunakan untuk menyelesaikan masalah yang berkaitan dengan tindakan sebuah unit bisnis (misalnya) untuk memenangkan persaingan dalam usaha yang digelutinya. Seperti diketahui, bahwa dalam praktek sehari-hari, setiap unit usaha atau organisasi pada umumnya harus berhadapan dengan para pesaing. Untuk memenangkan persaingan itulah, diperlukan analisis dan pemilihan strategi pemasaran tepat, khususnya strategi bersaing yang paling optimal bagi unit usaha atau organisasi yang bersangkutan.
Istilah pemrograman dinamis (dynamic programming) tentunya pernah kita dengar secara literatur, istilah ini banyak kita temui pada buku-buku algoritma komputer, riset operasional, ataupun buku yang berhubungan dengan matematika terapan. Sebagian orang juga mengenal Pemrograman dinamis sebagai suatu metode yang berkaitan dengan prinsip optimalisasi dan dapat diaplikasikan pada bidang industri, perbankan, hingga perencanaan network dan aplikasi perjalanan luar angkasa. Aplikasinya yang luas menjadikan pembahasan mengenai pemrograman dinamis menjadi suatu topik yang umum dan menarik. Untuk mencoba mengetahui lebih lanjut tentang pemrograman dinamis, pada artikel ini akan dibahas tentang dasar-dasar teori pemrograman dinamis secara singkat, juga dengan sejarah singkat dari asal mula istilah pemrograman dinamis.
Bioinformatika, sebagai salah satu bidang multidisiplin yang berkembang dan banyak menerapkan metode komputasi, tentunya menjadi bidang yang cukup terbuka terhadap suatu metode seperti metode pemrograman dinamis, lebih lanjut pada tulisan ini diterapkan aplikasi pemrograman dinamis sebagai metode optimalisasi dalam pemecahan masalah, dan dicontohkan pada masalah bilangan Fibonacci dan graf multitahap, pada akhirnya, sebagai penekanan dalam tulisan ini, adalah aplikasi pemrograman dinamis dalam bidang bioinformatika, khususnya pada algoritma Needleman-Wunsch untuk global sequence alignment.
Pemrograman Dinamis
Istilah Pemrograman Dinamis, pertama kali diperkenalkan pada era 1950-an oleh Richard Bellman seorang professor di Universitas Princeton dan juga bekerja pada RAND corporation, perlu diketahui bahwa RAND corporation pada era itu merupakan suatu perusahan yang dibentuk untuk menawarkan analisis dan riset untuk angkatan bersenjata Amerika Serikat. Pada saat itu, Bellman bekerja di bidang pengambilan keputusan multi tahap (multistage desicion process) dan mengerjakan beberapa metode matematis, beberapa tahun kemudian setelah Bellman berada di RAND, lahirlah istilah pemrograman dinamis. Istilah ini tidak secara langsung berhubungan dengan pemrograman, melainkan digunakan sebagai judul project yang kemudian yang diusulkan RAND coorporation pada Angkatan Udara Amerika Serikat. Selanjutnya, pada penerapanya pemrograman dinamis banyak digunakan pada proses optimalisasi masalah.
Pemrograman Dinamis merupakan sebuah algoritma pemecahan masalah dengan cara menguraikan solusi menjadi sekumpulan langkah atau tahapan sedemikian sehingga solusi dari persoalan dapat dipandang dari serangkaian keputusan yang saling berkaitan. Pada penyelesaian metode ini kita menggunakan persyaratan optimasi dan kendala untuk membatasi sejumlah pilihan yang harus dipertimbangkan pada suatu tahap. Algoritma Program Dinamis memiliki karakteristik sebagai berikut:
1.Persoalan dapat dibagi mejadi beberapa tahap, yang pada setiap tahap hanya diambil satu keputusan yang optimal.
2.Masing-masing tahap terdiri dari sejumlah status yang berhubungan dengan tahap tersebut.
3.Hasil keputusan yang diambil pada tahap ditransformasikan dari status yang bersangkutan ke status berikutnya pada tahap berikutnya.
4.Ongkos pada suatu tahap bergantung pada ongkos tahap-tahap sebelumnya dan meningkat secara teratur dengan bertambahnya jumlah tahapan
5.Keputusan terbaik pada suatu tahap bersifat independen terhadap keputusan yang dilakukan tahap sebelumnya.
6.Adanya hubungan rekursif yang mengidentifikasikan keputusan terbaik untuk setiap status pada tahap k memberikan keputusan terbaik untuk tahap sebelumnya.
7.Prinsip optimalitas berlaku pada persoalan tersebut.
Ciri utama dari Program Dinamis adalah prinsip optimalitas yang berbunyi “jika solusi total optimal, maka bagian solusi sampai tahap ke-k juga optimal”.
Dari karakteristik poin ke-4 di atas, kita dapat menyimpulkan bahwa algoritma Program Dinamis dapat diaplikasikan apabila peningkatkan ongkos secara linear dan diskrit sehingga optimasi parsial dapat dilakukan. Dalam menyelesaikan persoalan dengan Program Dinamis, kita dapat menggunakan 2 pendekatan berbeda yaitu :
a.Maju (forward atau up-down) : bergerak mulai dari tahap 1, terus maju ke tahap 2,3,..,n. Urutan variabel keputusan adalah x1,x2,…,xn
b.Mundur (backward atau bottom-up) : bergerak mulai dari tahap n, terus mundur ke tahap n-1, n-2,..,2,1. Urutan variabel keputusan adalah xn xn-1,x2,x1. Adapun kompleksitas waktu pada algoritma ini adalah O(| s1|*|s2|), jika panjang kedua string adalah ‘n’. Kompleksitas ruangnya juga sama jika seluruh matriks disimpan untuk merunut balik untuk mencari optimal alignment. Jika nilai edit distance dibutuhkan, hanya dua baris dari matriks yang dialokasi, matriks tersebut dapat mengalami ‘daur ulang’, dan kompleksitas ruangnya jadi O(n).
Adapun Dynamic programming adalah strategi untuk membangun masalah optimal bertingkat, yaitu masalah yang dapat digambarkan daalam bentuk serangkaian tahapan (stage) yang saling mempengaruhi. Umumnya tiap tahapan mempunyai 4 (empat) variabel yang mempunyai pengaruh, baik langsung maupun tidak langsung terhadap tahapan lainnya dari sistem
Adapun empat variabel tersebut adalah sebagai berikut :
1.Input untuk tahapan n, Xn, yang tergantung dari keputusan yang dibuat pada tahapan terdahulu atau tergantung dari input asal yang tetap pada system
2.Set keputusan pada tahap n, Dn yang menentukan kondisi atau syarat operasi dari tahapan.
3.Output dari tahapan n, Xn-1 yang biasa tergantung dari input pada tahapan n dan keputusan Dn.
4.Hasil dari tahapan n, Rn yang merupakan ukuran bagi konstribusi tahapan n terhadap fungsi tujuan sistem keseluruhan (ongkos, keuntungan, manfaat atau ukuran lain). Biasanya hasil ini merupakan gambaran dari suatu tahapan n dan output pada tahapan n.
